Estatística de Fermi-Dirac

Distribuição Fermi-Dirac como uma função de ε/μ num gráfico para 4 temperaturas diferentes. Ocupando transições são deriváveis a mais altas temperaturas.

Em mecânica estatística, a estatística de Fermi-Dirac é uma estatística quântica que rege as partículas de spin semi-inteiro, os férmions. Leva o nome de dois eminentes físicos: Enrico Fermi e Paul Adrien Maurice Dirac cada um dos quais descobriu o método de forma independente (embora Fermi tenha definido as estatísticas antes de Dirac).

Formulação matemática

A distribuição de Fermi-Dirac é dada por

$n_{i}(\epsilon ,T)={\frac {g_{i}}{e^{\frac {\epsilon -\mu }{k_{B}T}}+1}}$

Onde:

$n_{i}$ é o número médio de partículas no estado de energia $\epsilon _{i}$.

$g_{i}$ é a degenerescência do i-ésimo estado

$\epsilon _{i}$ é a energia no i-ésimo estado

$\mu$ é o potencial químico

$T$ é a temperatura

$k_{B}$ a constante de Boltzmann

Nos casos em que $\mu$ é a energia de Fermi $E_{F}\$ e $g_{i}=1\$, a função é chamada de função Fermi:

$F(E)={\frac {1}{e^{(\epsilon _{i}-E_{F})/kT}+1}}$

Fermi-Dirac distribution as a function of temperature. More states are occupied at higher temperatures.

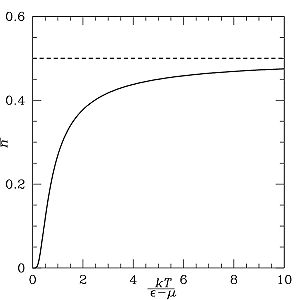
Interpretação física

1. Para baixas temperaturas, a distribução de Fermi é uma função de passo que vale 1 se $\epsilon <\mu$ e 0 se $\epsilon >\mu$. Isto quer dizer que as partículas vão se posicionando desde o nivel mais baixo de energia até acima devido ao princípio de exclusão de Pauli até que se tenham postas todas as partículas. A energia do último nível ocupado se denomina energia de Fermi e a temperatura à que corresponde esta energia mediante $\epsilon _{f}=k_{B}T_{f}$ , a temperatura de Fermi.

Se da circunstância de que a temperatura de Fermi da maioria dos metais reais é enorme (da ordem de 10000 Kelvin), portanto a aproximação de dizer que a distribução de Fermi-Dirac segue sendo um escalar até temperatura ambiente é válida com bastante precisão.

A distribuição de Fermi-Dirac tem importância capital no estudo de gases de férmions e em particular no estudo dos elétrons livres em um metal.

Aplicações

Estatísticas de Fermi–Dirac e Bose–Einstein aplicadas quando efeitos quânticos tendem a ser levadas em conta e as partículas são consideradas "indistinguíveis". Os efeitos quânticos aparecem se a concentração de partículas (N/V) ≥ n_q (aonde n_q é a concentração quântica). A concentração quântica é quando a distância interpartículas é igual ao comprimento de onda térmico de de Broglie, i.e. quando a funções de onda das partículas são atingidos mas não ultrapassados. Como a concentração quântica depende da temperatura; altas temperaturas irão colocar a maioria dos sistemas no limite clássico sem eles terem uma muito alta densidade, e.g. uma anã branca. A estatística de Fermi–Dirac é aplicada a férmions (partículas que obedecem ao princípio de exclusão de Pauli), a estatística de Bose–Einstein é aplicada a bósons. Tanto Fermi–Dirac e Bose–Einstein tornam-se a estatística de Maxwell–Boltzmann a altas temperaturas ou baixas concentrações.

Estatísticas de Maxwell–Boltzmann são frequentemente descritas como estatísticas de partículas clássicas "distinguíveis". Em outras palavras a configuração de partícula A no estado 1 e a partícula B no estado 2 é diferente do caso aonde a partícula B está no estado 1 e a partícula A está no estado 2. Quando esta idéia é estendida, conduz à distribuição própria (de Boltzmann)de partículas em estados de energia, mas conduz a resultados sem significado físico para a entropia, conforme encorporado no paradoxo de Gibbs. Estes problemas desaparecem quando se percebe que todas as partículas são de fato indistinguíveis entre sí. Ambas as distribuições se aproximam da distribuição de Maxwell-Boltzmann no limite de alta temperatura e baixa densidade, sem a necessidade de quaisquer pressupostos adicionais ad hoc. A distribuição estatística de Maxwell–Boltzmann é particularmente útil para estudar gases. A distribuição estatística de Fermi–Dirac é mais usualmente usada para o estudo do comportamento de elétrons em sólidos. Como tal, é a base da teoria dos dispositivos semicondutores e da eletrônica.

Ver também

• Estatística de Bose-Einstein
• Estatística de Maxwell–Boltzmann
• Férmion
• Princípio de exclusão de Pauli